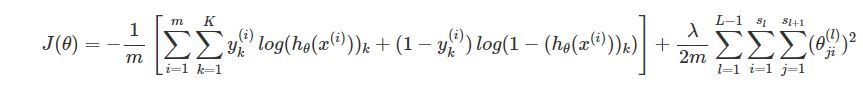Setting up image recognition problem
Credit to Andrew Ng (Stanford) and Serguei Maliar (Columbia) for portions of the code and data set.We are provided with some sample handwritten numbers. A sample of 100 numbers are provided below for visualization purposes.
These numbers range from 0 to 9, and each sample is divided into a 20 pixel by 20 pixel matrix, with each pixel being a feature in the input layer. This 20x20 matrix is then unspooled into a 400x1 vector. We intialize weights for this by generating 401 random theta values, corresponding to the 400 input features and 1 constant term.
For the hidden layer, we begin with a default of 25 nodes, and hence the weights for the hidden layer, Theta 2, has 26 random variables, corresponding to the 25 nodes and 1 constant term.
These data points are then fed into the neural network system with 0 regularization to calculate the cost of the neural network, using the below formula with regularization term:
We ignore the 2nd component of the function as Lambda has a value of 0 due to no regularization in the current neural network.
The default values gave us a cost of 0.287629. Introducing a default regularization constant of 1 increases cost to 0.383770.
We then implement backpropagation in the neural network to derive the error associated with each input and hidden layer node. The neural network is then trained over multiple iterations to minimize cost by changing theta values. A visualization of the weights provided by the default neural network is below:
We then use the model to predict the values of each handwritten digit, deriving an accuracy of 95%. A sample of the prediction is below:
Following this, I made an attempt to improve on model accuracy by increasing the number of hidden layer nodes from 25 to 50. This increased the number of Theta 2 values from 26 to 51. Running over the same iterative neural network training method with similar starting Theta 1 and 2 guesses resulted in a 99.84% model accuracy.
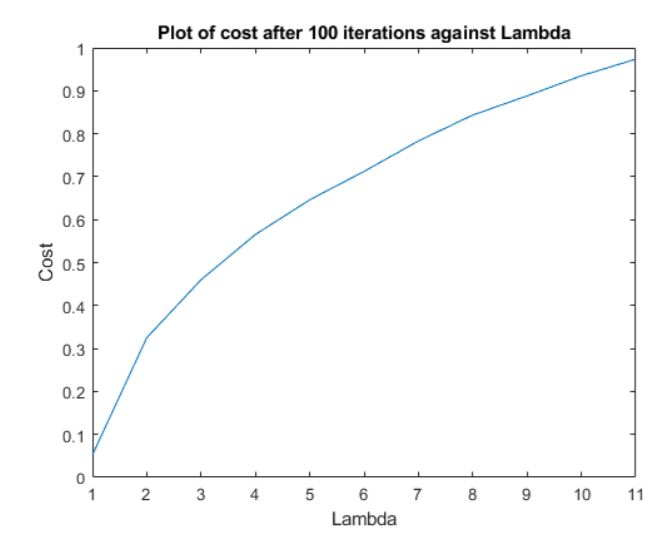
Notably, I ran a test on optimal regularization constant which suggests that an integer constant of 0 would be the most optimal, as any regularization constant increases the optimal cost of the system.
All in, this was an extremely interesting exercise demonstrating the power of neural network in solving problems such as handwritting recognition.
Of some note is that the data we received is largely relatively clean, with few “problematic” writing samples. For example, with longer string of numbers, we could have overlaps. It is also possible in a real world setting for people to have very strange handwriting, or ‘noise’ around the number such as spilled ink, coffee stains etc. which could all add complexity to the network.
This is an interesting problem that I hope to have the chance to explore in the future.