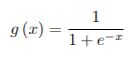Machine Learning - Neural Network and Image Recognition Part 1

Neural Network Introduction

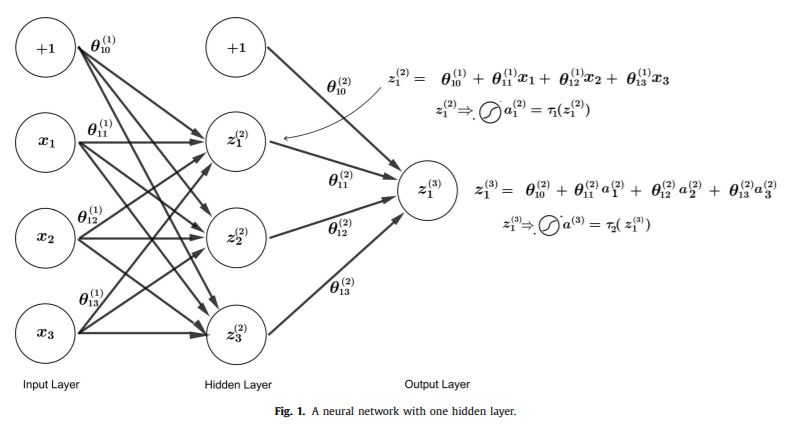
Neural networks are powerful tools in assisting with machine learning, consisting of input, hidden, and output layers. Each individual neuron node within a hidden layer can be a representation of a logistic, linear or perceptron function. The neural network itself can have multiple neurons and hidden layers, culminating in a desired output. A sample neural network with 1 hidden layer is shown below.

Image credit: Serguei Maliar, Columbia University

The input layer consists of a constant term, denoted by the +1 node, as well as three features, (x1,x2,x3). These inputs are multiplied by various theta weights in separate calculations to derive z values, (z1,z2,z3). The z values then serve as activation thresholds through linear, logistic or perceptron functions, deriving activation signals (a1,a2,a3). The a values are then used as inputs with their own corresponding coefficients in calculating z1 in the output layer. This z1 then serves as activation threshold for the final function, giving us our final result.

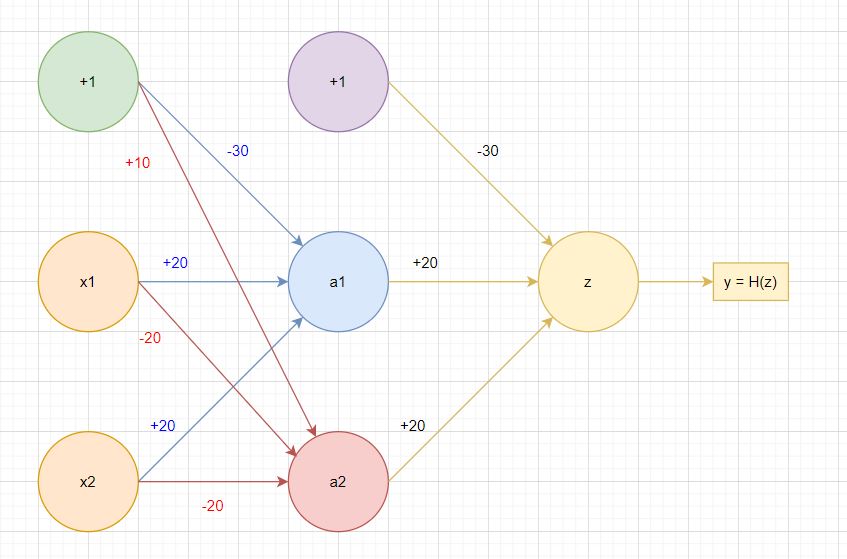
A sample XOR function is below, demonstrating the use of neural network logic gates. Assuming a 2 variable sample set (x1,x2) where variables can take the values of true (1) or false (0). We want to set up a logic gate to check for exclusive or (XOR), i.e. an odd number of variables are true. A possible set of weights and functions are below:

Drawn by author on draw.io

The two nodes in the hidden layer are fed inputs using various weights.

For node a1, we have z1 = -30 + 20x1 + 20x2.

For node a2, we have z2 = +10 - 20x1 - 20x2.

The activation function for each a node is a logistic sigmoid function, taking the form below:

If both x1 and x2 values are true, we see z1 = -30 + 20 + 20 = 10, and z2 = +10 - 20 - 20 = -30. Hence, using z1 and z2 as inputs in the sigmoid function, we get a1 approximately equal to 1, and a2 approximately equal to 0.

a1 and a2 are then used as inputs in calculating z in the output layer, where z = -30 + 20a1 + 20a2. In our above example where both x1 and x2 values are true, and a1 = 1, a2 = 0, z = -30 + 20 + 0 = -10.

y (our final output) is calculated via sigmoid function as well, giving us a y value of approximately 0. This matches expectations of our XOR gate, since both x1 and x2 are true, we expect a final output for XOR of false (0).

In part 2, I will be looking into use of neural networks in image recognition problems.

A fun tool to visualize neural networks and their effects is TensorFlow Playground